Newton-Cotes rules for integration¶
We briefly discuss the simplest integration of a function from an evaluation of the integrand at equally spaced points.
We want to integrate $f(x)$ in the interval $[a,b]$ with $N$ points, $\Delta = (b-a)/N$.
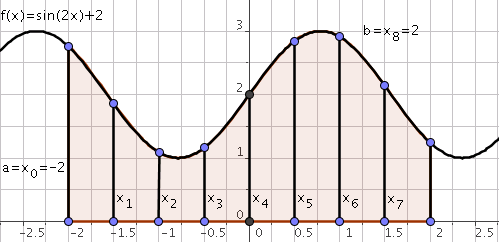
Rectangular¶
\begin{equation*} \int_a^b f(x) dx = \Delta \sum_{j=0}^{N-1} f \left( a + j \Delta \right) + \mathcal{O}\left(\frac{1}{N}\right). \end{equation*}
Trapezoidal¶
\begin{equation*} \int_a^b f(x) dx = \Delta \left [\frac{1}{2}f(a) + \sum_{j=1}^{N-1} f\left(a + j \Delta \right) +\frac{1}{2}f(b)\right] + \mathcal{O}\left(\frac{1}{N^2}\right). \end{equation*}
Simpson¶
\begin{equation*} \int_a^b f(x) dx = \frac{\Delta}{3} \left \{ f(a) + \sum_{j=1}^{N-1}\left[3-(-1)^j\right] f\left(a + j \Delta \right) +f(b)\right\} + \mathcal{O}\left(\frac{1}{N^4}\right). \end{equation*}
Error in Newton-Cotes methods¶
- Difference between exact result and quadrature with $N$ points for \begin{equation*} \frac{2}{\sqrt{\pi}} \int_0^{1/2} \mathrm{e}^{-t^2} dt \end{equation*}
What happens in higher dimensions?¶
A method of order $k$ has an error $\sim 1 / N^k$.
For example, Simpson's method is order $k=4$.
This is OK in 1 dimension. But what about $d$ dimensions?
\begin{equation*} I = \int_{\Omega} d^d x\, f(\mathbf{x}) = \int dx_1 \int dx_2 \cdots \int dx_d\, f(\mathbf{x}). \end{equation*}
We need $M$ points in every dimension for a total of $N = M^d$ points.
The error $\sim 1/M^k$.
What about a Monte Carlo approach?¶
Let's take our pebbles: every throw is described by a random variable $x_i$
\begin{equation*} \langle x_i \rangle = \frac{\pi}{4} \cdot 4 + \left( 1 - \frac{\pi}{4} \right) \cdot 0 = \pi \qquad \langle x^2_i \rangle = 4\pi \qquad \sigma = \sqrt{4\pi-\pi^2} \end{equation*}
Empirical average $X$
\begin{equation*} X = \frac{1}{N} \sum_{i=1}^N x_i \qquad \langle X \rangle = \frac{1}{N} \sum_{i=1}^N \langle x_i \rangle = \pi \end{equation*}
What is the standart deviation on the empirical average?
\begin{equation*} \langle X^2 \rangle - \langle X \rangle^2 = \frac{1}{N^2} \sum_{i,j=1}^N \langle x_i x_j \rangle - \frac{1}{N^2} \sum_{i,j} \langle x_i \rangle \langle x_j \rangle = \frac{1}{N} \sigma^2 \Rightarrow \quad \boxed{\sigma_X = \frac{\sigma}{\sqrt{N}}} \end{equation*}